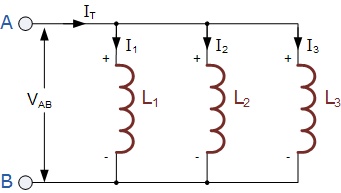
La chute de tension sur tous les inducteurs en parallèle sera la même. Ainsi, les inducteurs en parallèle ont une tension commune qui les traverse et dans notre exemple ci-dessous, la tension à travers les inducteurs est donnée comme suit :

V_L1 = V_L2 = V_L3 = V_AB …etc

Dans le circuit suivant, les inducteurs L₁, L₂ et L₃ sont tous connectés en parallèle entre les deux points A et B.

Circuit d’Inducteurs en Parallèle

Dans le tutoriel précédent sur les inducteurs en série, nous avons vu que l’inductance totale, L_T, du circuit était égale à la somme de tous les inducteurs individuels. Pour les inducteurs connectés en parallèle, l’inductance équivalente du circuit L_T est calculée différemment.

La somme des courants individuels passant à travers chaque inducteur peut être trouvée en utilisant la loi des courants de Kirchhoff (KCL) où, I_T = I₁ + I₂ + I₃ et nous savons d’après les tutoriels précédents que l’EMF auto-induit dans un inducteur est donné par : V = L di/dt

En prenant les valeurs des courants individuels passant à travers chaque inducteur dans notre circuit ci-dessus, et en remplaçant le courant i par i₁ + i₂ + i₃, la tension à travers la combinaison parallèle est donnée comme suit :

En substituant di/dt dans l’équation ci-dessus par v/L, nous obtenons :

Nous pouvons réduire cela pour donner une expression finale pour calculer l’inductance totale d’un circuit parallèle, et celle-ci est donnée comme suit :

Équation de l’Inducteur en Parallèle

Ici, comme pour les calculs d’une résistance en parallèle, les valeurs réciproques ( 1/Ln ) des inductances individuelles sont toutes additionnées au lieu des inductances elles-mêmes. Mais encore une fois, comme pour les inductances en série, l’équation ci-dessus n’est vraie que lorsqu’il n’y a “AUCUNE” inductance mutuelle ou couplage magnétique entre deux ou plusieurs des inducteurs, (ils sont magnétiquement isolés les uns des autres). Lorsque le couplage entre les bobines est présent, l’inductance totale est également affectée par le degré de couplage.

Cette méthode de calcul peut être utilisée pour calculer n’importe quel nombre d’inductances individuelles connectées ensemble dans un seul réseau parallèle. Cependant, s’il n’y a que deux inductances individuelles connectées en parallèle, une formule beaucoup plus simple et rapide peut être utilisée pour trouver la valeur totale de l’inductance, et celle-ci est :

Un point important à retenir concernant les circuits inductifs parallèles est que l’inductance totale ( L_T ) de deux ou plusieurs inducteurs connectés ensemble en parallèle sera toujours INFÉRIEURE à la valeur de la plus petite inductance dans la branche parallèle.

Exemple de Tutoriel N°1

Trois inducteurs de 60mH, 120mH et 75mH respectivement, sont connectés ensemble dans une combinaison parallèle sans inductance mutuelle entre eux. Calculez l’inductance totale de la combinaison parallèle en millihenries.

Inducteurs Parallèles Couplés Mutuellement

Lorsque des inducteurs sont connectés ensemble en parallèle de manière à ce que le champ magnétique de l’un soit lié à l’autre, l’effet de l’inductance mutuelle augmente ou diminue l’inductance totale selon le degré de couplage magnétique qui existe entre les bobines. L’effet de cette inductance mutuelle dépend de la distance entre les bobines et de leur orientation l’une par rapport à l’autre.

Les inducteurs parallèles connectés mutuellement peuvent être classés comme étant soit « aidants » soit « opposés » à l’inductance totale, les bobines en parallèle aidantes augmentant l’inductance équivalente totale et les bobines en parallèle opposées diminuant l’inductance équivalente totale par rapport à celles qui n’ont pas d’inductance mutuelle.

Les bobines parallèles couplées mutuellement peuvent être représentées comme étant connectées dans une configuration aidante ou opposée à l’aide de points de polarité ou de marqueurs de polarité comme montré ci-dessous.

Inducteurs Aidants en Parallèle

La tension à travers les deux inducteurs aidants ci-dessus doit être égale puisqu’ils sont en parallèle, donc les deux courants, i₁ et i₂, doivent varier de sorte que la tension à travers eux reste la même. L’inductance totale, L_T, pour deux inducteurs aidants en parallèle est donnée par :

Où : 2M représente l’influence de la bobine L ₁ sur L ₂ et vice versa pour la bobine L ₂ sur L ₁.

Si les deux inductances sont égales et que le couplage magnétique est parfait, comme dans un circuit toroïdal, alors l’inductance équivalente des deux inducteurs en parallèle est L car L_T = L₁ = L₂ = M. Cependant, si l’inductance mutuelle entre elles est nulle, l’inductance équivalente serait L ÷ 2, la même que pour deux inducteurs auto-induits.

Si l’une des deux bobines était inversée par rapport à l’autre, alors nous aurions deux inducteurs parallèles opposés et l’inductance mutuelle, M, qui existe entre les deux bobines aura un effet annulant sur chaque bobine au lieu d’un effet aidant comme montré ci-dessous.

Inducteurs Opposés en Parallèle

Alors, l’inductance totale, L_T, pour deux inducteurs parallèles opposés est donnée par :

Cette fois, si les deux inductances sont de valeur égale et que le couplage magnétique est parfait entre elles, l’inductance équivalente et l’EMF auto-induite à travers les inducteurs seront nulles car les deux inducteurs s’annulent mutuellement.

Cela est dû au fait que lorsque les deux courants, i₁ et i₂, passent à travers chaque inducteur à tour de rôle, le flux mutuel total généré entre eux est nul car les deux flux produits par chaque inducteur sont égaux en magnitude mais opposés en direction.

Ainsi, les deux bobines deviennent effectivement un court-circuit pour le flux de courant dans le circuit, de sorte que l’inductance équivalente, L_T, devient égale à ( L ± M ) ÷ 2.

Exemple de Tutoriel N°2

Deux inducteurs de 75mH et 55mH respectivement sont connectés ensemble en parallèle aidant. Leur inductance mutuelle est donnée comme 22.5mH. Calculez l’inductance totale.

Exemple de Tutoriel N°3

Calculez l’inductance équivalente du circuit inductif suivant.

Calculez la première branche d’inducteur L_A, (Inducteur L₅ en parallèle avec les inducteurs L₆ et L₇)

Calculez la deuxième branche d’inducteur L_B, (Inducteur L₃ en parallèle avec les inducteurs L₄ et L_A)

Calculez l’inductance équivalente du circuit L_EQ, (Inducteur L₁ en parallèle avec les inducteurs L₂ et L_B)

L’inductance équivalente pour le circuit ci-dessus a été trouvée comme : 15mH.

Résumé du Tutoriel

Comme avec la résistance, les inducteurs connectés ensemble en parallèle ont la même tension, V qui les traverse. De plus, connecter des inducteurs en parallèle diminue l’inductance effective du circuit, l’inductance équivalente de “N” inducteurs connectés en parallèle étant le réciproque de la somme des réciproques des inductances individuelles.

Tout comme dans les inducteurs en série, les inducteurs connectés mutuellement en parallèle sont classés comme étant soit « aidants » soit « opposés » à cette inductance totale, en fonction de si les bobines sont couplées cumulativement (dans la même direction) ou différentiellement (dans des directions opposées).

Jusqu’à présent, nous avons examiné l’inducteur en tant que composant passif pur ou idéal. Dans le prochain tutoriel sur les inducteurs, nous examinerons des inducteurs non idéaux qui ont des bobines résistives réelles produisant le circuit équivalent d’un inducteur en série avec une résistance et examinerons la constante de temps de tel circuit.