L’Algèbre Booléenne et ses Lois
L’algèbre booléenne utilise un ensemble de lois et de règles pour définir le fonctionnement d’un circuit logique numérique.
Un ensemble de règles ou de lois des expressions booléennes a été inventé pour aider à réduire le nombre de portes logiques nécessaires à l’exécution d’une opération logique particulière, ce qui résulte en une liste de fonctions ou de théorèmes communément appelés les Lois de l’Algèbre Booléenne.
En plus des symboles logiques « 0 » et « 1 » utilisés pour représenter une entrée ou une sortie numérique, nous pouvons également les utiliser comme constantes pour un circuit ou un contact étant « Ouvert » ou « Fermé » de manière permanente, respectivement.
L’Algèbre Booléenne est la mathématique que nous utilisons pour analyser les portes et circuits numériques. Nous pouvons utiliser ces Lois de l’Algèbre Booléenne pour réduire et simplifier une expression booléenne complexe dans le but de diminuer le nombre de portes logiques requises. L’algèbre booléenne est donc un système de mathématiques basé sur la logique qui possède son propre ensemble de règles ou lois qui sont utilisées pour définir et réduire des expressions booléennes.
Les variables utilisées dans l’Algèbre Booléenne n’ont qu’une des deux valeurs possibles, un « 0 » logique et un « 1 » logique, mais une expression peut avoir un nombre infini de variables, chacune étiquetée individuellement pour représenter des entrées pour l’expression. Par exemple, les variables A, B, C, etc., nous donnent une expression logique de A + B = C, mais chaque variable ne peut être qu’un 0 ou un 1.
Des exemples de ces lois, règles et théorèmes individuels de l’algèbre booléenne sont donnés dans le tableau suivant.
Tableaux de Vérité
| Expression Booléenne | Description | Circuit de Commutation Équivalent | Loi ou Règle de L’Algèbre Booléenne |
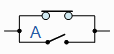
| A + 1 = 1 | A en parallèle avec fermé = “FERMÉ” |  | Annulation |
| A + 0 = A | A en parallèle avec ouvert = “A” |  | Identité |
| A . 1 = A | A en série avec fermé = “A” |  | Identité |
| A . 0 = 0 | A en série avec ouvert = “OUVERT” |  | Annulation |
| A + A = A | A en parallèle avec A = “A” |  | Idempotent |
| A . A = A | A en série avec A = “A” |  | Idempotent |
| NOT A = A | NOT NOT A (double négatif) = “A” | Double Négation | |
| A + A = 1 | A en parallèle avec NOT A = “FERMÉ” |  | Complément |
| A . A = 0 | A en série avec NOT A = “OUVERT” |  | Complément |
| A+B = B+A | A en parallèle avec B = B en parallèle avec A |  | Commutatif |
| A.B = B.A | A en série avec B = B en série avec A |  | Commutatif |
| A+B = A.B | inverse et remplacer OU par ET | Théorème de de Morgan | |
| A.B = A+B | inverse et remplacer ET par OU | Théorème de de Morgan |
Les Lois de l’Algèbre Booléenne qui se rapportent à la Loi Commutative permettant un changement de position pour l’addition et la multiplication, la Loi Associative permettant la suppression des parenthèses pour l’addition et la multiplication, ainsi que la Loi Distributive permettant le factorisation d’une expression, sont les mêmes que dans l’algèbre ordinaire.
Chacune des Lois Booléennes ci-dessus est donnée avec seulement une ou deux variables, mais le nombre de variables définies par une seule loi n’est pas limité, car il peut y avoir un nombre infini de variables comme entrées pour l’expression. Ces lois booléennes détaillées ci-dessus peuvent être utilisées pour prouver toute expression booléenne donnée ainsi que pour simplifier des circuits numériques compliqués.
Une brève description des diverses Lois de l’Algèbre Booléenne est donnée ci-dessous avec A représentant une entrée variable.
Description des Lois de l’Algèbre Booléenne
- Loi d’Annulation – Un terme ET‘é avec un « 0 » équivaut à 0 ou OU‘é avec un « 1 » équivaut à 1
- A . 0 = 0 Une variable ET‘ée avec 0 est toujours égale à 0
- A + 1 = 1 Une variable OU‘ée avec 1 est toujours égale à 1
- Loi d’Identité – Un terme OU‘é avec un « 0 » ou ET‘é avec un « 1 » sera toujours égal à ce terme
- A + 0 = A Une variable OU‘ée avec 0 est toujours égale à la variable
- A . 1 = A Une variable ET‘ée avec 1 est toujours égale à la variable
- Loi Idempotente – Une entrée qui est ET‘ée ou OU´ée avec elle-même est égale à cette entrée
- A + A = A Une variable OU‘ée avec elle-même est toujours égale à la variable
- A . A = A Une variable ET‘ée avec elle-même est toujours égale à la variable
- Loi de Complément – Un terme ET‘é avec son complément équivaut à « 0 » et un terme OU´é avec son complément équivaut à « 1 »
- A . A = 0 Une variable ET‘ée avec son complément est toujours égale à 0
- A + A = 1 Une variable OU‘ée avec son complément est toujours égale à 1
- Loi Commutative – L’ordre d’application de deux termes séparés n’est pas important
- A . B = B . A L’ordre dans lequel deux variables sont ET’ées n’a pas d’importance
- A + B = B + A L’ordre dans lequel deux variables sont OU’ées n’a pas d’importance
- Loi de Double Négation – Un terme qui est inversé deux fois est égal au terme original
- A = A Un double complément d’une variable est toujours égal à la variable
- Théorème de de Morgan – Il existe deux règles ou théorèmes de « de Morgan »
- (1) Deux termes séparés NOR‘és ensemble sont équivalents aux deux termes inversés (Complément) et ET‘és par exemple : A+B = A . B
- (2) Deux termes séparés NAND‘és ensemble sont équivalents aux deux termes inversés (Complément) et OU‘és par exemple : A.B = A + B
D’autres lois algébriques de l’algèbre booléenne non détaillées ci-dessus comprennent :
- Postulats Booléens – Bien qu’ils ne soient pas des lois booléennes à part entière, ce sont un ensemble de lois mathématiques qui peuvent être utilisées dans la simplification des expressions booléennes.
- 0 . 0 = 0 Un 0 ET’é avec lui-même est toujours égal à 0
- 1 . 1 = 1 Un 1 ET’é avec lui-même est toujours égal à 1
- 1 . 0 = 0 Un 1 ET’é avec un 0 est égal à 0
- 0 + 0 = 0 Un 0 OU’é avec lui-même est toujours égal à 0
- 1 + 1 = 1 Un 1 OU’é avec lui-même est toujours égal à 1
- 1 + 0 = 1 Un 1 OU’é avec un 0 est égal à 1
- 1 = 0 L’inverse (complément) d’un 1 est toujours égal à 0
- 0 = 1 L’inverse (complément) d’un 0 est toujours égal à 1
- Loi Distributive – Cette loi permet de multiplier ou de factoriser une expression.
- A(B + C) = A.B + A.C (OU Loi Distributive)
- A + (B.C) = (A + B).(A + C) (ET Loi Distributive)
- Loi d’Avoir – Cette loi permet une réduction d’une expression compliquée à une expression plus simple en absorbant des termes similaires.
- A + (A.B) = (A.1) + (A.B) = A(1 + B) = A (OU Loi d’Avoir)
- A(A + B) = (A + 0).(A + B) = A + (0.B) = A (ET Loi d’Avoir)
- Loi Associative – Cette loi permet la suppression des parenthèses d’une expression et le regroupement des variables.
- A + (B + C) = (A + B) + C = A + B + C (OU Loi Associative)
- A(B.C) = (A.B)C = A . B . C (ET Loi Associative)
Fonctions de l’Algèbre Booléenne
En utilisant les informations ci-dessus, des portes simples à 2 entrées AND, OR et NOT peuvent être représentées par 16 fonctions possibles comme indiqué dans le tableau suivant.
| Fonction | Description | Expression |
| 1. | NULL | 0 |
| 2. | IDENTITÉ | 1 |
| 3. | Entrée A | A |
| 4. | Entrée B | B |
| 5. | NON A | A |
| 6. | NON B | B |
| 7. | A ET B (AND) | A . B |
| 8. | A ET NON B | A . B |
| 9. | NON A ET B | A . B |
| 10. | NON ET (NAND) | A . B |
| 11. | A OU B (OR) | A + B |
| 12. | A OU NON B | A + B |
| 13. | NON A OU B | A + B |
| 14. | NON OU (NOR) | A + B |
| 15. | Exclusive-OR | A . B + A . B |
| 16. | Exclusive-NOR | A . B + A . B |
Exemple de Loi de l’Algèbre Booléenne No1
En utilisant les lois ci-dessus, simplifions l’expression suivante : (A + B)(A + C)
| Q = | (A + B).(A + C) | |
| A.A + A.C + A.B + B.C | – Loi distributive | |
| A + A.C + A.B + B.C | – Loi idempotente (A.A = A) | |
| A(1 + C) + A.B + B.C | – Loi distributive | |
| A.1 + A.B + B.C | – Loi d’identité (1 + C = 1) | |
| A(1 + B) + B.C | – Loi distributive | |
| A.1 + B.C | – Loi d’identité (1 + B = 1) | |
| Q = | A + (B.C) | – Loi d’identité (A.1 = A) |
Alors l’expression : (A + B)(A + C) peut être simplifiée en A + (B.C) comme dans la loi distributive.