Nombres binaires signés
Les nombres binaires signés utilisent le bit de poids fort (MSB) comme un bit de signe pour afficher une plage de nombres positifs ou négatifs.
En mathématiques, les nombres positifs (y compris zéro) sont représentés comme des nombres non signés. Nous ne mettons donc pas le signe + devant eux pour indiquer qu’ils sont positifs. Cependant, lorsqu’il s’agit de nombres négatifs, nous utilisons un signe – devant le nombre pour montrer que ce nombre est négatif en valeur et différent d’une valeur non signée positive, et il en va de même pour les nombres binaires signés.
Cependant, dans les circuits numériques, il n’y a pas de disposition pour mettre un signe plus ou même un signe moins à un nombre, puisque les systèmes numériques fonctionnent avec des nombres binaires représentés en termes de « 0 » et « 1 ». Lorsqu’ils sont utilisés ensemble en microélectronique, ces « 1 » et « 0 », appelés un bit (étant une contraction de BInaire digiT), tombent dans plusieurs tailles de plages de nombres qui sont référencées par des noms communs, tels qu’un octet ou un mot.
Nous avons également vu précédemment qu’un nombre binaire de 8 bits (un octet) peut avoir une valeur allant de 0 (000000002) à 255 (111111112), c’est-à-dire 28 = 256 combinaisons différentes de bits formant un seul octet de 8 bits. Par exemple, un nombre binaire non signé tel que : 010011012 = 64 + 8 + 4 + 1 = 7710 en décimal. Mais les systèmes numériques et les ordinateurs doivent également être capables d’utiliser et de manipuler des nombres négatifs ainsi que des nombres positifs.
Les nombres mathématiques se composent généralement d’un signe et d’une valeur (magnitude) dans laquelle le signe indique si le nombre est positif, ( + ) ou négatif, ( – ) avec la valeur indiquant la taille du nombre, par exemple 23, +156 ou -274. Présenter des nombres de cette manière est appelé représentation « signe-magnitude », car le chiffre le plus à gauche peut être utilisé pour indiquer le signe et les chiffres restants la magnitude ou la valeur du nombre.
La notation signe-magnitude est la méthode la plus simple et l’une des plus courantes pour représenter des nombres positifs et négatifs des deux côtés de zéro, (0). Ainsi, les nombres négatifs sont obtenus simplement en changeant le signe du nombre positif correspondant, car chaque nombre positif ou non signé aura un opposé signé, par exemple, +2 et -2, +10 et -10, etc.
Mais comment représentons-nous des nombres binaires signés si tout ce que nous avons est une série de zéros et de uns ? Nous savons que les chiffres binaires, ou bits n’ont que deux valeurs, soit un « 1 » ou un « 0 » et, commodément pour nous, un signe n’a également que deux valeurs, étant un « + » ou un « – ».
Nous pouvons alors utiliser un seul bit pour identifier le signe d’un nombre binaire signé comme étant positif ou négatif en valeur. Pour représenter un nombre binaire positif (+n) et un nombre binaire négatif (-n), nous pouvons les utiliser avec l’ajout d’un signe.
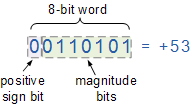
Pour les nombres binaires signés, le bit de poids fort (MSB) est utilisé comme le bit de signe. Si le bit de signe est « 0 », cela signifie que le nombre est positif en valeur. Si le bit de signe est « 1 », alors le nombre est négatif en valeur. Les bits restants dans le nombre sont utilisés pour représenter la magnitude du nombre binaire de la manière habituelle du format de nombre binaire non signé.
Ensuite, nous pouvons voir que la notation Signe-et-Magnitude (SM) stocke des valeurs positives et négatives en divisant les « n » bits totaux en deux parties : 1 bit pour le signe et n–1 bits pour la valeur qui est un nombre binaire pur. Par exemple, le nombre décimal 53 peut être exprimé comme un nombre binaire signé de 8 bits comme suit.
Nombres binaires signés positifs

Nombres binaires signés négatifs

L’inconvénient ici est qu’alors qu’auparavant nous avions une plage complète de nombres binaires non signés de n bits, nous avons maintenant un nombre binaire signé de n-1 bits ce qui donne une plage réduite de chiffres allant de :
-2(n-1) à +2(n-1)
Donc, par exemple : si nous avons 4 bits pour représenter un nombre binaire signé, (1 bit pour le bit de signe et 3 bits pour les bits de magnitude), alors la plage réelle de nombres que nous pouvons représenter en notation signe-magnitude serait :
-2(4-1) – 1 à +2(4-1) – 1
-2(3) – 1 à +2(3) – 1
-7 à +7
Alors qu’auparavant, la plage d’un nombre binaire non signé de 4 bits aurait été de 0 à 15, ou 0 à F en hexadécimal, nous avons maintenant une plage réduite de -7 à +7. Ainsi, un nombre binaire non signé n’a pas de bit de signe unique, et peut donc avoir une plus grande plage binaire car le bit de poids fort (MSB) est juste un bit ou un chiffre supplémentaire plutôt qu’un bit de signe utilisé.
Un autre inconvénient ici de la forme signe-magnitude est que nous pouvons avoir un résultat positif pour zéro, +0 ou 00002, et un résultat négatif pour zéro, -0 ou 10002. Les deux sont valides mais lequel est correct.
Exemple de Nombres Binaires Signés No1
Convertir les valeurs décimales suivantes en nombres binaires signés en utilisant le format de signe-magnitude :
| -1510 comme un nombre de 6 bits | ⇒ | 1011112 |
| +2310 comme un nombre de 6 bits | ⇒ | 0101112 |
| -5610 comme un nombre de 8 bits | ⇒ | 101110002 |
| +8510 comme un nombre de 8 bits | ⇒ | 010101012 |
| -12710 comme un nombre de 8 bits | ⇒ | 111111112 |
Notez que pour un nombre binaire signé de 4 bits, 6 bits, 8 bits, 16 bits ou 32 bits, tous les bits DOIVENT avoir une valeur, donc des “0” sont utilisés pour remplir les espaces entre le bit de signe le plus à gauche et la première valeur « 1 » la plus élevée.
La représentation signe-magnitude d’un nombre binaire est une méthode simple à utiliser et à comprendre pour représenter des nombres binaires signés, car nous utilisons ce système tout le temps avec les nombres décimaux normaux (base 10) en mathématiques. Ajouter un « 1 » devant si le nombre binaire est négatif et un « 0 » s’il est positif.
Cependant, utiliser cette méthode de signe-magnitude peut entraîner la possibilité que deux modèles de bits différents aient la même valeur binaire. Par exemple, +0 et -0 seraient 0000 et 1000 respectivement en tant que nombre binaire signé de 4 bits.
Nous pouvons donc voir qu’en utilisant cette méthode, il peut y avoir deux représentations pour zéro, un zéro positif ( 00002 ) et également un zéro négatif ( 10002 ) ce qui peut causer de grandes complications pour les ordinateurs et les systèmes numériques.
Complément à un Nombre Binaire Signé
Complément à un ou Complément de 1 comme il est parfois appelé, est une autre méthode que nous pouvons utiliser pour représenter des nombres binaires négatifs dans un système de nombres binaires signés. Dans le complément à un, les nombres positifs (également connus sous le nom de non-compléments) restent inchangés comme auparavant avec les nombres de signe-magnitude.
Cependant, les nombres négatifs sont représentés en prenant le complément à un du nombre positif non signé. Puisque les nombres positifs commencent toujours par un « 0 », le complément commencera toujours par un « 1 » pour indiquer un nombre négatif.
Le complément à un d’un nombre binaire négatif est le complément de son équivalent positif, donc pour prendre le complément à un d’un nombre binaire, tout ce que nous devons faire est de changer chaque bit à son tour. Ainsi, le complément à un de « 1 » est « 0 » et vice versa, donc le complément à un de 100101002 est simplement 011010112 car tous les 1 sont changés en 0 et les 0 en 1.
Le moyen le plus facile de trouver le complément à un d’un nombre binaire signé lors de la construction de circuits arithmétiques ou de décodeurs logiques numériques est d’utiliser des Inverseurs. L’inverseur est naturellement un générateur de complément et peut être utilisé en parallèle pour trouver le complément à 1 de tout nombre binaire comme démontré.
Complément à 1 utilisant des inverseurs

Nous pouvons donc voir qu’il est très facile de trouver le complément à un d’un nombre binaire N car tout ce que nous devons faire est simplement de changer les 1 en 0 et les 0 en 1 pour nous donner un équivalent -N. De plus, tout comme la précédente représentation signe-magnitude, le complément à un peut également avoir une notation de n bits pour représenter des nombres dans la plage de : -2(n-1) et +2(n-1) – 1.
Par exemple, une représentation de 4 bits dans le format du complément à un peut être utilisée pour représenter les nombres décimaux dans la plage de -7 à +7 avec deux représentations de zéro : 0000 (+0) et 1111 (-0) comme avant.
Addition et Soustraction Utilisant le Complément à Un
L’un des principaux avantages du Complément à Un est dans l’addition et la soustraction de deux nombres binaires. En mathématiques, la soustraction peut être mise en œuvre de diverses manières comme A – B, c’est la même chose que de dire A + (-B) ou -B + A, etc. Par conséquent, la complication soustrayant deux nombres binaires peut être effectuée en utilisant simplement l’addition.
Nous avons vu dans le tutoriel sur l’Addition Binaire que l’addition binaire suit les mêmes règles que pour l’addition normale, sauf que dans le binaire, il n’y a que deux bits (chiffres) et le plus grand chiffre est un « 1 », (tout comme « 9 » est le plus grand chiffre décimal), ainsi les combinaisons possibles pour l’addition binaire sont les suivantes :
| 0 | 0 | 1 | 1 | |
| + 0 | + 1 | + 0 | + 1 | |
| 0 | 1 | 1 | 1← 0 | ( 0 plus une retenue 1 ) |
Lorsque les deux nombres à additionner sont tous deux positifs, la somme A + B, ils peuvent être additionnés ensemble par la somme directe (y compris le nombre et le bit de signe), car lorsque des bits uniques sont ajoutés ensemble, « 0 + 0 », « 0 + 1 », ou « 1 + 0 » donne une somme de « 0 » ou « 1 ».
Cela est dû au fait que lorsque les deux bits que nous voulons additionner sont impairs (« 0 » + « 1 » ou « 1 + 0 »), le résultat est « 1 ». De même, lorsque les deux bits à additionner sont pairs (« 0 + 0 » ou « 1 + 1 »), le résultat est « 0 » jusqu’à ce que vous obteniez « 1 + 1 », alors la somme est égale à « 0 » plus une retenue « 1 ». Examinons un exemple simple.
Soustraction de Deux Nombres Binaires
Un système numérique de 8 bits est requis pour soustraire les deux nombres suivants 115 et 27 l’un de l’autre en utilisant le complément à un. Donc en décimal, cela serait : 115 – 27 = 88.
Tout d’abord, nous devons convertir les deux nombres décimaux en binaire et nous assurer que chaque nombre a le même nombre de bits en ajoutant des zéros en tête pour produire un nombre de 8 bits (octet). Donc :
11510 en binaire est : 011100112
2710 en binaire est : 000110112
Maintenant, nous devons trouver le complément du deuxième nombre binaire, (00011011) tout en laissant le premier nombre (01110011) inchangé. Donc en changeant tous les 1 en 0 et les 0 en 1, le complément à un de 00011011 est donc égal à 11100100.
Ajouter le premier nombre et le complément du deuxième nombre donne :
| 01110011 |
| + 11100100 |
| Débordement → 1 01010111 |
Puisque le système numérique doit travailler avec 8 bits, seuls les huit premiers chiffres sont utilisés pour fournir la réponse à la somme, et nous ignorons simplement le dernier bit (bit 9). Ce bit est appelé un bit de « débordement ». Le débordement se produit lorsque la somme de la colonne la plus significative (la plus à gauche) produit une retenue. Ce bit de débordement ou de retenue peut être complètement ignoré ou passé à la section numérique suivante pour être utilisé dans ses calculs. Le débordement indique que la réponse est positive. S’il n’y a pas de débordement, alors la réponse est négative.
Le résultat de 8 bits d’au-dessus est : 01010111 (le débordement « 1 » s’annule) et pour le convertir de nouveau d’une réponse de complément à un à la réponse réelle, nous devons maintenant ajouter « 1 » au résultat de complément à un, donc :
| 01010111 |
| + 1 |
| 01011000 |
Donc le résultat de la soustraction de 27 (000110112) de 115 (011100112) en utilisant le complément à un en binaire donne la réponse de : 010110002 ou (64 + 16 + 8) = 8810 en décimal.
Ensuite, nous pouvons voir que les nombres binaires signés ou non signés peuvent être soustraits les uns des autres en utilisant le Complément à Un et le processus d’addition. Des additions binaires telles que le TTL 74LS83 ou 74LS283 peuvent être utilisées pour additionner ou soustraire deux nombres binaires signés de 4 bits ou sont connectées ensemble pour produire des additions de 8 bits complètes avec un débordement.
Complément à Deux
Complément à Deux ou Complément de 2 comme il est aussi appelé, est une autre méthode semblable à la précédente forme de signe-magnitude et au complément à un que nous pouvons utiliser pour représenter des nombres binaires négatifs dans un système de nombres binaires signés. Dans le complément à deux, les nombres positifs sont exactement les mêmes que précédemment pour les nombres binaires non signés. Un nombre négatif, cependant, est représenté par un nombre binaire, qui, lorsqu’il est additionné à son équivalent positif correspondant, donne zéro.
Dans le format du complément à deux, un nombre négatif est le complément à 2 de son nombre positif, avec la soustraction de deux nombres étant A – B = A + (complément à 2 de B), utilisant pratiquement le même procédé qu’auparavant, car fondamentalement, le complément à deux est le complément à un + 1.
L’avantage principal du complément à deux sur le complément à un précédent est qu’il n’y a pas de problème de double zéro plus il est beaucoup plus facile de générer le complément à deux d’un nombre binaire signé. Par conséquent, les opérations arithmétiques sont relativement plus faciles à effectuer lorsque les nombres sont représentés dans le format complément à deux.
Regardons la soustraction de nos deux nombres de 8 bits, 115 et 27, de ci-dessus en utilisant le complément à deux, et nous nous souvenons de ci-dessus que les équivalents binaires sont :
11510 en binaire est : 011100112
2710 en binaire est : 000110112
Nos nombres font 8 bits, alors il y a 28 chiffres disponibles pour représenter nos valeurs et en binaire cela égale : 1000000002 ou 25610. Puis le complément à deux de 2710 sera :
(28)2 – 00011011 = 100000000 – 00011011 = 111001012
Le complément du deuxième nombre négatif signifie que la soustraction devient une addition beaucoup plus facile des deux nombres, alors la somme est : 115 + (complément à 2 de 27) qui est :
01110011 + 11100101 = 1 010110002
Comme auparavant, le 9ème bit de débordement est ignoré puisque nous ne sommes intéressés que par les 8 premiers bits, donc le résultat est : 010110002 ou (64 + 16 + 8) = 8810 en décimal, le même que précédemment.
Résumé du Tutoriel
Nous avons vu que les nombres binaires négatifs peuvent être représentés en utilisant le bit de poids fort (MSB) comme un bit de signe. Si un nombre binaire de n bits est signé, le bit le plus à gauche est utilisé pour représenter le signe laissant n-1 bits pour représenter le nombre.
Par exemple, dans un nombre binaire de 4 bits, cela laisse seulement 3 bits pour contenir le véritable nombre. Si cependant, le nombre binaire est non signé, alors tous les bits peuvent être utilisés pour représenter le nombre.
La représentation d’un nombre binaire signé est généralement appelée notation signe-magnitude et si le bit de signe est « 0 », le nombre est positif. Si le bit de signe est « 1 », alors le nombre est négatif. Lorsqu’il s’agit d’opérations arithmétiques binaires, il est plus pratique d’utiliser le complément du nombre négatif.
La complémentation est un moyen alternatif de représenter des nombres binaires négatifs. Ce système de codage alternatif permet la soustraction des nombres négatifs en utilisant simplement l’addition.
Puisque les nombres à signe positif en notation signe-magnitude commencent toujours par un zéro (0), son complément commencera donc toujours par un un (1) pour indiquer un nombre négatif comme indiqué dans le tableau suivant.
Comparaison des Nombres Binaires Signés de 4 bits
| Décimal | Signe Magnitude | Complément à Un Signé | Complément à Deux Signé |
| +7 | 0111 | 0111 | 0111 |
| +6 | 0110 | 0110 | 0110 |
| +5 | 0101 | 0101 | 0101 |
| +4 | 0100 | 0100 | 0100 |
| +3 | 0011 | 0011 | 0011 |
| +2 | 0010 | 0010 | 0010 |
| +1 | 0001 | 0001 | 0001 |
| +0 | 0000 | 0000 | 0000 |
| -0 | 1000 | 1111 | – |
| -1 | 1001 | 1110 | 1111 |
| -2 | 1010 | 1101 | 1110 |
| -3 | 1011 | 1100 | 1101 |
| -4 | 1100 | 1011 | 1100 |
| -5 | 1101 | 1010 | 1011 |
| -6 | 1110 | 1001 | 1010 |
| -7 | 1111 | 1000 | 1001 |
Les formes de complément des nombres binaires signés peuvent utiliser soit le complément à un soit le complément à deux. Le complément à un et le complément à deux d’un nombre binaire sont importants car ils permettent la représentation des nombres négatifs.
La méthode de l’arithmétique du complément à deux est couramment utilisée dans les ordinateurs pour gérer les nombres négatifs, le seul inconvénient est que si nous voulons représenter des nombres binaires négatifs dans le format de nombre binaire signé, nous devons renoncer à une partie de la plage du nombre positif que nous avions auparavant.