Les données dans les circuits numériques et les ordinateurs sont stockées et transmises sous forme d’une série de zéros et de uns. Différents systèmes de numérotation sont ainsi utilisés pour représenter ces données. Les nombres binaires, ayant uniquement deux chiffres (0 et 1), permettent à chaque donnée (nombre) d’être représentée de manière efficace.

Contrairement à un circuit linéaire ou analogique, tel que les amplificateurs AC qui traitent des signaux variant en amplitude ou fréquence, les circuits numériques traitent des signaux contenant seulement deux niveaux de tension, appelés logique “0” et logique “1”.

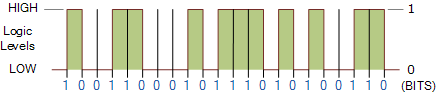
De manière générale, une logique “1” représente une tension plus élevée, comme 5 volts, couramment appelée valeur HAUTE, tandis qu’une logique “0” représente une tension plus basse, comme 0 volts ou la terre, connue sous le nom de valeur BASSE. Ces deux niveaux de tension discrets représentant les valeurs numériques “1” (un) et “0” (zéro) sont couramment appelés : BInary digiTS, et dans les circuits et applications numériques et informatiques, ils sont normalement appelés BITS binaires.

Bits binaires de zéros et de uns

La présence de seulement deux valeurs booléennes valides pour représenter soit une logique “1” soit une logique “0” rend le système d’utilisation des Nombres Binaires idéal pour les circuits et systèmes électroniques ou numériques.

Le système de numération binaire est un système de numération de base 2 qui suit les mêmes règles mathématiques que le système décimal ou base-10 couramment utilisé. Ainsi, au lieu des puissances de dix, (b>10ⁿ ), par exemple : 1, 10, 100, 1000, les nombres binaires utilisent des puissances de deux, (2ⁿ ) doublant effectivement la valeur de chaque bit successif, par exemple : 1, 2, 4, 8, 16, 32, etc.

Les tensions utilisées pour représenter un circuit numérique peuvent être de n’importe quelle valeur, mais généralement dans les systèmes numériques et informatiques, elles sont maintenues bien en dessous de 10 volts. Dans les systèmes numériques, ces tensions sont appelées “niveaux logiques” et idéalement un niveau de tension représente un état “HAUT”, tandis qu’un autre niveau de tension différent et plus bas représente un état “BAS”. Un système de numération binaire utilise ces deux états.

Les formes d’onde ou signaux numériques consistent en niveaux de tension discrets ou distincts qui changent entre ces deux états “HAUT” et “BAS”. Mais qu’est-ce qui rend un signal ou une tension “numérique” et comment pouvons-nous représenter ces niveaux de tension “HAUT” et “BAS”? Les circuits et systèmes électroniques peuvent être divisés en deux catégories principales.

• • Circuits Analogiques – Les circuits analogiques ou linéaires amplifient ou répondent à des niveaux de tension variant continuellement entre une valeur positive et négative sur une période de temps.
• • Circuits Numériques – Les circuits numériques produisent ou répondent à deux niveaux de tension distincts, positifs ou négatifs, représentant soit un niveau logique “1”, soit un niveau logique “0”.

Nombres Binaires – Sortie de Tension Analogique

Un exemple simple des différences entre un circuit analogique et un circuit numérique est montré ci-dessous :

Représentation de la Sortie de Tension Analogique

Ceci est un circuit analogique. La sortie du potentiomètre varie à mesure que la borne du balai est tournée, produisant un nombre infini de points de tension entre 0 volts et V_MAX. La tension de sortie peut varier lentement ou rapidement d’une valeur à l’autre, il n’y a donc pas de changement soudain ou progressif entre deux niveaux de tension, produisant ainsi une tension de sortie continuellement variable. Des exemples de signaux analogiques incluent température, pression, niveaux de liquide et intensité lumineuse.

Nombres Binaires – Sortie de Tension Numérique

Dans cet exemple de circuit numérique, le balai du potentiomètre a été remplacé par un seul interrupteur rotatif qui est connecté à chaque nœud de la chaîne de résistances en série, formant un réseau de diviseur de potentiel basique.

Ainsi, lorsque l’interrupteur est tourné d’une position (ou nœud) à la suivante, la tension de sortie, V_OUT, change rapidement en niveaux de tension discrets et distincts représentant des multiples de 1.0 volts à chaque action ou étape de commutation, comme montré dans le graphique de sortie.

Par exemple, la tension de sortie sera de 2 volts, 3 volts, 5 volts, etc. mais PAS 2.5V, 3.1V ou 4.6V. Des niveaux de tension de sortie plus fins pourraient être facilement produits en utilisant un interrupteur multi-positions et en augmentant le nombre d’éléments résistifs dans le réseau de diviseur de potentiel, augmentant ainsi le nombre d’étapes de commutation discrètes.

Représentation de la Sortie de Tension Numérique

Nous pouvons alors voir que la principale différence entre un signal ou une quantité analogique et une quantité numérique est qu’une quantité “analogique” change continuellement dans le temps, tandis qu’une quantité “numérique” a des valeurs discrètes (étape par étape). “BAS” à “HAUT” ou “HAUT” à “BAS”.

Un bon exemple de cela serait un variateur de lumière dans votre maison qui fait varier l’intensité lumineuse (luminosité) vers le haut ou vers le bas alors qu’il est tourné entre complètement ALLUMÉ (luminosité maximale) et complètement ÉTEINT, produisant une sortie analogique qui varie continuellement. D’autre part, avec un interrupteur mural standard, la lumière est soit “ALLUMÉE” (HAUT) soit “ÉTEINTE” (BAS) lorsque l’interrupteur est actionné. Le résultat est qu’il n’y a pas de milieu produisant une forme de sortie numérique ON-OFF.

Certains circuits combinent à la fois des signaux analogiques et numériques, comme un convertisseur analogique-numérique (CAN) ou un convertisseur numérique-analogique (CNA). Quoi qu’il en soit, le signal d’entrée ou de sortie numérique représente une valeur numérique binaire équivalente à un signal analogique.

Nombres Binaires – Niveaux Logiques Numériques

Dans tous les circuits électroniques et informatiques, seules deux niveaux logiques sont autorisés pour représenter un état unique. Ces niveaux sont appelés logique 1 ou logique 0, HAUT ou BAS, Vrai ou Faux, ALLUMÉ ou ÉTEINT. La plupart des systèmes logiques utilisent une logique positive, dans ce cas, une logique “0” est représentée par zéro volts et une logique “1” est représentée par une tension plus élevée. Par exemple, +5 volts pour la logique TTL comme montré.

Représentation de la Valeur Numérique

Premier État	Deuxième État
Logique “0”	Logique “1”
BAS	HAUT
FAUX	VRAI
Sortie de Tension de Bas Niveau	Sortie de Tension de Haut Niveau
0V ou Terre	+5 Volts

En général, la commutation d’un niveau de tension, “>&0” à “1” ou “1” à “0” doit être effectuée aussi rapidement que possible pour éviter les mauvaises commutations du circuit logique. Dans les circuits intégrés TTL (logique transistor-transistor), il existe une plage prédéfinie de limites de tensions d’entrée et de sortie pour définir ce qu’est exactement une valeur logique “1” et ce qu’est une valeur logique “0”.

Niveaux de Tension TTL d’Entrée et de Sortie

Lorsque l’on utilise une alimentation de +5 volts, toute tension d’entrée entre 2.0v et 5v est reconnue comme une valeur logique “1”, et toute tension d’entrée inférieure à 0.8v est reconnue comme une valeur logique “0”. Tandis que la sortie d’une porte logique entre 2.7v et 5v représente une valeur logique “1”, et une tension de sortie inférieure à 0.4v représente une valeur logique “0”. Cela est appelé “logique positive” et est utilisé dans ces tutoriels sur la logique numérique.

Les nombres binaires sont couramment utilisés dans les circuits numériques et informatiques et sont représentés soit par une logique “0” soit par une logique “1”. Les systèmes de numération binaire sont les mieux adaptés au codage numérique des signaux binaires, car ils n’utilisent que deux chiffres, un et zéro, pour former différentes figures. Dans cette section sur les nombres binaires, nous examinerons la conversion des nombres décimaux ou de base-10 en nombres octaux, hexadécimaux et binaires.

Dans le prochain tutoriel sur les Nombres Binaires et le système de numération binaire, nous traiterons de la conversion des nombres décimaux en nombres binaires, et vice versa, et introduirons le concept du Byte et du Word pour représenter les parties d’un nombre binaire beaucoup plus grand.